指数级增长是什么意思_指数级增长和几何级增长区别
投资币 · 2024-11-26 01:13
指数级增长是一种在每个时期内数量以非常快的速度增长的现象,其增长速度比一般的线性增长要快。指数级增长的定义是:每经过一个时间段发展,数量以极快的速度增加,如果在两个时期之间可以将数量乘以一个常数,则称为指数级增长。
一个典型的指数增长函数可以表示为 y=a×b^x,其中a为数量初值,b为比例因子,x为时间,y为时间到达x时的数量。它说明,数量随时间的改变而呈现指数级别的增长。
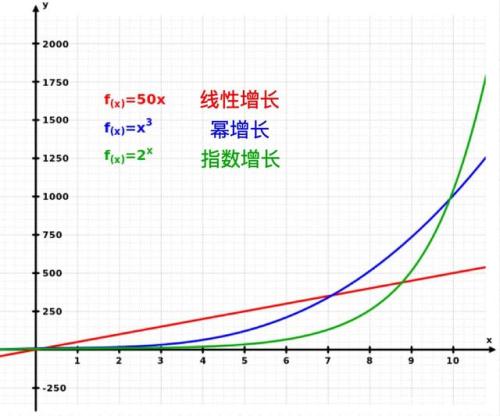
指数级增长的现象在多个领域都有出现,如金融投资、网络数据和计算力、存储力和传输力的增长等。随着时间的推移,这些领域的数量增长速度越来越快,呈现出指数级别的趋势。
在金融领域,指数级增长可以用于描述投资收益的增长,随着时间的推移,投资的收益增长越来越快。在股票市场中,这种增长方式又被称为滚雪球效应,即越操作,投资者所能赚取的收益就越大。
在数字化时代,摩尔定律与梅特卡夫定律两个指数型增长效应叠加,释放出巨大能量。摩尔定律描述了数字化计算能力每两年疯狂成倍增长的规律,而梅特卡夫定律则描述了网络的价值与网络中节点数的平方成正比的增长规律。
指数级增长和几何级增长区别:
1.变化速度:指数级增长的变化速度非常快,随着数据量的增加,其增长速度会迅速加快。相比之下,几何级增长的变化速度相对缓慢,每一项的增长速度都相对较小。
2.增长方式:指数级增长基于指数运算,通常表示为a×x^y,其中x是底数,y是指数。而几何级增长则基于乘法运算,每一项与前一项的比值相等。在几何上,面积与边长的关系是乘积的函数关系,因此也将成倍增长称为“几何级数增长”。
相关文章
Relevent